4. Two-Dimensional Solver
4.1. Dimensional Splitting
1. Two-Dimensional Splitting
There are no changes needed to be done to the F-Wave solver, because two-dimensional splitting is used i.e, first calculating the x-direction than the y-direction.
Therefore only changes will be done in WavePropagation2d.
The constructor and destructor of WavePropagation2d is very similar to WavePropagation1d except the new variables:
m_hvfor y-momentum
m_xCells&m_yCellsfor the number of x and y cells
stridethe size in x-direction including ghost cells
totalCellstotal number of cells including ghost cells
The functions that needed to be changed compared to WavePropagation2d are the get-functions, timeStep and setGhostOutflow.
get-functions
The get-functions now need to take the stride into account i.e. the first row need to be completely skip because ghost cells are not returned.
setGhostOutflow
In the first for loop, the ghost cells are set in the y direction, except for the first and last row (ghost rows), by taking their value from the value of their left/right neighbor. In the second loop, the first and last rows (ghost rows) are set by taking the value from the lower and upper neighbor. In both loops the activated reflection is taken into account.
// Header: WavePropagation2d.h
// File: WavePropagation2d.cpp
// Test: WavePropagation2d.test.cpp
void tsunami_lab::patches::WavePropagation2d::setGhostOutflow()
{
t_real* l_h = m_h[m_step];
t_real* l_hu = m_hu[m_step];
t_real* l_hv = m_hv[m_step];
for( t_idx i = 1; i < m_yCells + 1; i++ )
{
t_idx y = stride * i;
// set left boundary
l_h[y] = l_h[y + 1] * !hasReflection[Side::LEFT];
l_hu[y] = l_hu[y + 1];
l_hv[y] = l_hv[y + 1];
m_bathymetry[y] = m_bathymetry[y + 1];
// set right boundary
l_h[y + m_xCells + 1] = l_h[y + m_xCells] * !hasReflection[Side::RIGHT];
l_hu[y + m_xCells + 1] = l_hu[y + m_xCells];
l_hv[y + m_xCells + 1] = l_hv[y + m_xCells];
m_bathymetry[y + m_xCells + 1] = m_bathymetry[y + m_xCells];
}
for( size_t i = 0; i < stride; i++ )
{
// set top complete row of ghost cells
t_idx waterRowT = stride + i;
l_h[i] = l_h[waterRowT] * !hasReflection[Side::TOP];
l_hu[i] = l_hu[waterRowT];
l_hv[i] = l_hv[waterRowT];
m_bathymetry[i] = m_bathymetry[waterRowT];
// set bottom complete row of ghost cells
t_idx ghostRowB = ( m_yCells + 1 ) * stride + i;
t_idx waterRowB = m_yCells * stride + i;
l_h[ghostRowB] = l_h[waterRowB] * !hasReflection[Side::BOTTOM];
l_hu[ghostRowB] = l_hu[waterRowB];
l_hv[ghostRowB] = l_hv[waterRowB];
m_bathymetry[ghostRowB] = m_bathymetry[waterRowB];
}
}
timeStep
First the update is done in x-direction.
Therefore the height and x-momentum arrays are initialized.
The first for loop counts in y-direction and the second for loop counts in x-direction.
Then the index of the left and right cells are calculated.
The next steps are the same as performed in WavePropagation1d.
// File: WavePropagation2d.cpp
// pointers to old and new data
t_real* l_hOld = m_h[m_step];
t_real* l_huOld = m_hu[m_step];
m_step = ( m_step + 1 ) % 2;
t_real* l_hNew = m_h[m_step];
t_real* l_huNew = m_hu[m_step];
// init new cell quantities
for( t_idx l_ce = 0; l_ce < totalCells; l_ce++ )
{
l_hNew[l_ce] = l_hOld[l_ce];
l_huNew[l_ce] = l_huOld[l_ce];
}
// only possible for f-wave solver
if( hasBathymetry )
{
// iterates through the row
for( t_idx i = 0; i < m_yCells + 1; i++ )
{
// iterates along the row
for( t_idx j = 0; j < m_xCells + 1; j++ )
{
t_idx k = stride * i + j;
// determine left and right cell-id
t_idx l_ceL = k;
t_idx l_ceR = k + 1;
// noting to compute both shore cells
if( l_hOld[l_ceL] == 0 && l_hOld[l_ceR] == 0 )
{
continue;
}
// compute reflection
t_real heightLeft;
t_real heightRight;
t_real momentumLeft;
t_real momentumRight;
t_real bathymetryLeft;
t_real bathymetryRight;
Reflection reflection = calculateReflection( l_hOld,
l_huOld,
l_ceL,
l_ceR,
heightLeft,
heightRight,
momentumLeft,
momentumRight,
bathymetryLeft,
bathymetryRight );
// compute net-updates
t_real l_netUpdates[2][2];
tsunami_lab::solvers::FWave::netUpdates( heightLeft,
heightRight,
momentumLeft,
momentumRight,
bathymetryRight,
bathymetryLeft,
l_netUpdates[0],
l_netUpdates[1] );
// update the cells' quantities
l_hNew[l_ceL] -= i_scaling * l_netUpdates[0][0] * ( Reflection::RIGHT != reflection );
l_huNew[l_ceL] -= i_scaling * l_netUpdates[0][1] * ( Reflection::RIGHT != reflection );
l_hNew[l_ceR] -= i_scaling * l_netUpdates[1][0] * ( Reflection::LEFT != reflection );
l_huNew[l_ceR] -= i_scaling * l_netUpdates[1][1] * ( Reflection::LEFT != reflection );
}
}
}
else
{
// uses a function pointer to choose between the solvers
void ( *netUpdates )( t_real, t_real, t_real, t_real, t_real*, t_real* ) = solvers::FWave::netUpdates;
if( solver == Solver::ROE )
{
netUpdates = solvers::Roe::netUpdates;
}
[ ... ]
}
Then the h buffers are swapped to load the m_h and m_hv from the same step.
Thus the new results for m_h, m_hu, m_hv are located in the same step.
//swapping the h buffer new and old to write new data in previous old
m_h[m_step] = l_hOld;
m_step = ( m_step + 1 ) % 2;
m_h[m_step] = l_hNew;
// pointers to old and new data
t_real* l_hvOld = m_hv[m_step];
l_hOld = m_h[m_step];
m_step = ( m_step + 1 ) % 2;
t_real* l_hvNew = m_hv[m_step];
l_hNew = m_h[m_step];
// copy the calculated cell quantities
for( t_idx l_ce = 0; l_ce < totalCells; l_ce++ )
{
l_hNew[l_ce] = l_hOld[l_ce];
l_hvNew[l_ce] = l_hvOld[l_ce];
}
The calculation in the y-direction follows the same principle, but now we have to take a full stride to the next cell, i.e. we use the top and bottom cells for the update. To make this calculation more efficient, 32 values in the x-direction are updated simultaneously in the y-direction. This is done to address a 128-byte cache line, i.e. \(\text{sizeof(float)} \cdot 32 = 4 \text{ byte} \cdot 32 = 128 \text{ byte}\). Otherwise, three loaded values would be lost if the arrays are aligned correctly. If the cache line is smaller than 128 bytes, e.g. 64 bytes or 32 bytes, then values are loaded that would also be loaded later. However, the number of simultaneously updated values in the y-direction should not be too large, otherwise loaded values from the lower cells that are needed in the next iteration will be wasted.
To change the value used, which makes the calculation more efficient as explained above, the variable ITERATIONS_CACHE is used.
In this case, ITERATIONS_CACHE is 32, which will be used for the rest of the explanation.
The implementation requires two loops.
The first loop iterates over all cells in the x-direction as long as the number of cells is divisible by 32.
The next inner loop iterates over the rows, and the last inner loop is used to make the calculation more efficient.
The indices of the top and bottom cells to be updated are then determined.
The second loop deals with the remaining cells in the x direction that are less than 32.
The loop iterates over the rows and the inner loop over the remaining cells in the x-direction, using the same calculations as the first loop.
The calculation of reflection and update are the same as performed in WavePropagation1d.
// calculates xCells dividable by ITERATIONS_CACHE and remaining cells
t_idx full_xCells = ( m_xCells / ITERATIONS_CACHE ) * ITERATIONS_CACHE;
t_idx remaining_xCells = m_xCells % ITERATIONS_CACHE;
// only possible for f-wave solver
if( hasBathymetry )
{
// iterates over the x direction
for( t_idx i = 1; i < full_xCells; i += ITERATIONS_CACHE )
{
// iterate over the rows i.e. y-coordinates
for( t_idx j = 0; j < m_yCells + 1; j++ )
{
// iterations for more efficient cache usage
for( t_idx k = 0; k < ITERATIONS_CACHE; k++ )
{
// determine left and right cell-id
t_idx l_ceT = stride * j + i + k;
t_idx l_ceB = stride * ( j + 1 ) + i + k;
// noting to compute both shore cells
if( l_hOld[l_ceT] == 0 && l_hOld[l_ceB] == 0 )
{
continue;
}
// compute reflection
t_real heightLeft;
t_real heightRight;
t_real momentumLeft;
t_real momentumRight;
t_real bathymetryLeft;
t_real bathymetryRight;
Reflection reflection = calculateReflection( l_hOld,
l_hvOld,
l_ceT,
l_ceB,
heightLeft,
heightRight,
momentumLeft,
momentumRight,
bathymetryLeft,
bathymetryRight );
// compute net-updates
t_real l_netUpdates[2][2];
tsunami_lab::solvers::FWave::netUpdates( heightLeft,
heightRight,
momentumLeft,
momentumRight,
bathymetryRight,
bathymetryLeft,
l_netUpdates[0],
l_netUpdates[1] );
// update the cells' quantities
l_hNew[l_ceT] -= i_scaling * l_netUpdates[0][0] * ( Reflection::RIGHT != reflection );
l_hvNew[l_ceT] -= i_scaling * l_netUpdates[0][1] * ( Reflection::RIGHT != reflection );
l_hNew[l_ceB] -= i_scaling * l_netUpdates[1][0] * ( Reflection::LEFT != reflection );
l_hvNew[l_ceB] -= i_scaling * l_netUpdates[1][1] * ( Reflection::LEFT != reflection );
}
}
}
// iterate over the rows i.e. y-coordinates
for( t_idx j = 0; j < m_yCells + 1; j++ )
{
// remaining iterations for more efficient cache usage
for( t_idx k = 0; k < remaining_xCells; k++ )
{
// determine left and right cell-id
t_idx l_ceT = stride * j + full_xCells + k;
t_idx l_ceB = stride * ( j + 1 ) + full_xCells + k;
// noting to compute both shore cells
if( l_hOld[l_ceT] == 0 && l_hOld[l_ceB] == 0 )
{
continue;
}
// compute reflection
t_real heightLeft;
t_real heightRight;
t_real momentumLeft;
t_real momentumRight;
t_real bathymetryLeft;
t_real bathymetryRight;
Reflection reflection = calculateReflection( l_hOld,
l_hvOld,
l_ceT,
l_ceB,
heightLeft,
heightRight,
momentumLeft,
momentumRight,
bathymetryLeft,
bathymetryRight );
// compute net-updates
t_real l_netUpdates[2][2];
tsunami_lab::solvers::FWave::netUpdates( heightLeft,
heightRight,
momentumLeft,
momentumRight,
bathymetryRight,
bathymetryLeft,
l_netUpdates[0],
l_netUpdates[1] );
// update the cells' quantities
l_hNew[l_ceT] -= i_scaling * l_netUpdates[0][0] * ( Reflection::RIGHT != reflection );
l_hvNew[l_ceT] -= i_scaling * l_netUpdates[0][1] * ( Reflection::RIGHT != reflection );
l_hNew[l_ceB] -= i_scaling * l_netUpdates[1][0] * ( Reflection::LEFT != reflection );
l_hvNew[l_ceB] -= i_scaling * l_netUpdates[1][1] * ( Reflection::LEFT != reflection );
}
}
}
else
{
// uses a function pointer to choose between the solvers
void ( *netUpdates )( t_real, t_real, t_real, t_real, t_real*, t_real* ) = solvers::FWave::netUpdates;
if( solver == Solver::ROE )
{
netUpdates = solvers::Roe::netUpdates;
}
[ ... ]
}
2. Circular Dam Break
The circular dam break setup is implemented by a standard constructor with hard coded values from the example:
There is also a constructor with which the circular dam break can be adjusted, i.e. the height of the center, the height outside the center, the position of the center and the scale of the center can be set.
The height is set according to the calculation in the example, which creates a circle on a 2D plane. The momentum and bathymetry functions return zero, as none of these functions are set in this setup.
// Header: CircularDamBreak2d.h
// File: CircularDamBreak2d.cpp
// Test: CircularDamBreak2d.test.cpp
tsunami_lab::t_real tsunami_lab::setups::CircularDamBreak2d::getHeight( t_real i_x,
t_real i_y ) const
{
bool isInside = std::sqrt( std::pow( i_x - locationCenter[0], 2 ) + std::pow( i_y - locationCenter[1], 2 ) ) < scaleCenter;
return isInside ? heightCenter : heightOutside;
}
Visualizing the circular dam break without bathymetry with 500 x 500 cells.
3. Bathymetry & Obstacle
Visualizing the bathymetry effects with 500 x 500 cells.

The red lines on the left and right indicate that the wave in the x-direction propagates more slowly than the wave in the y-direction because there is a dent in the bathymetry in the center in y-direction. Otherwise, the waves in the x and y directions should hit the simulation boundary at the same time, as can be seen in the video circular dam break at about 3 seconds. The bathymetry is therefore also taken into account in the 2D simulation.
Visualizing the bathymetry with and obstacle effects with 500 x 500 cells. Reflection at the wall can be seen at about 1 second.
4.2. Stations
1. tsunami_lab::io::Stations
“When solving wave propagation problems, we are often times interested in output at specific points (or stations) of the computational domain. A station is defined by its coordinates \(s=(x,y)\) and is used to measure the water level at frequent intervals of seconds. a frequent interval of seconds.”[1]
New class `tsunami_lab::io::Stations summarizes a collection of user-defined stations.
We enter the number of cells in x and y direction and the scale in x and y direction to later calculate the indices of the queried position at which the station is located.
/// File: Stations.cpp
/// Header: Stations.h
/// Test: Stations.test.cpp
namespace fs = std::filesystem;
const std::string SOLUTION_FOLDER = "solutions";
tsunami_lab::io::Stations::Stations( t_idx i_nx,
t_idx i_ny,
t_idx i_stride,
t_real i_scaleX,
t_real i_scaleY )
{
m_nx = i_nx;
m_ny = i_ny;
m_stride = i_stride;
m_scaleX = i_scaleX;
m_scaleY = i_scaleY;
m_time = 0;
[ ... ]
To get the user-defined station we have to include the header #include <nlohmann/json.hpp>
which allows us to read data from our config.json. To not use the actual .json config in our test cases we decide between
config.test.json and config.json at the beginning.
/// File: Stations.cpp
[ ... ]
#ifdef TSUNAMI_SIMULATION_TEST
std::ifstream l_file( "resources/config.test.json" );
#endif // TSUNAMI_SIMULATION_TEST
#ifndef TSUNAMI_SIMULATION_TEST
std::ifstream l_file( "resources/config.json" );
#endif // !TSUNAMI_SIMULATION_TEST
json config;
try
{
l_file >> config;
}
catch( const std::exception& e )
{
std::cerr << "Error parsing JSON: " << e.what() << std::endl;
exit( 1 );
}
[ ... ]
We are saving the output of every station in a separate .csv file. First we check if the directory in which the data is saved exists. If it exists we delete the direction and in booth cases we are creating a new one with the old name. The same process with the single .csv files. Thus we are allways creating new data for every simulation.
/// File: Stations.cpp
[ ... ]
// create station folder inside solution folder
if( !fs::exists( SOLUTION_FOLDER ) )
{
fs::create_directory( SOLUTION_FOLDER );
}
if( fs::exists( SOLUTION_FOLDER + "/station" ) )
{
fs::remove_all( SOLUTION_FOLDER + "/station" );
}
fs::create_directory( SOLUTION_FOLDER + "/station" );
[ ... ]
Now everything is set up and we can add every station which is defined in the config.json to our Stations class
which will manage them. First of all we read the output frequency which all stations share. It specifies the time
in seconds of the write operations to the stations comma-separated files.
To simplify everything we defined in Stations.h a struct which saves the attributes of a station:
/// File: Stations.h
[ ... ]
struct Station
{
/**
* struct to save attributes of single station
*
* @param i_name name of station
* @param i_x x-coordinate of station
* @param i_y y-coordinate of station
* @param i_path path to the station file to be written to
*/
Station( std::string i_name, t_real i_x, t_real i_y, std::string i_path )
: m_name( i_name ), m_x( i_x ), m_y( i_y ), m_path( i_path )
{
}
//! name of station
std::string m_name;
//! x-coordinate of station
t_real m_x;
//! y-coordinate of station
t_real m_y;
//! path to the station file to be written to
std::string m_path;
};
[ ... ]
Afterwards we iterate over the json array stations in which the single stations are specified and gather the name,
x-coordinate and y-coordinate of every station. The structures are then added to a vector to summarizes all stations.
/// File: Stations.cpp
[ ... ]
if( config.contains( "output_frequency" ) )
m_outputFrequency = config["output_frequency"];
// add stations
if( config.contains( "stations" ) )
{
for( size_t i = 0; i < config["stations"].size(); i++ )
{
std::string l_name = config["stations"][i]["name"];
t_real l_x = config["stations"][i]["x"];
t_real l_y = config["stations"][i]["y"];
std::string l_path = SOLUTION_FOLDER + "/station/" + l_name;
std::ofstream l_fileStation;
l_fileStation.open( l_path, std::ios::app );
l_fileStation << "timestep,totalHeight" << "\n";
// forward arguments and construct station directly in the vector
m_stations.emplace_back( l_name, l_x, l_y, l_path );
}
}
}
Now we need a write method which is used to write the current values to the respective csv files of the stations. At the moment we only write a timestamp together with the current water level in the csv files. To do this, we enter a pointer to the array with the current water levels in the write method. Since we internally calculate with a different number of cells than the user provides for the simulation, we first calculate the actual index of the cell in the array from the scale and the number of user-defined cells. We then read this value and write it to the corresponding file together with a timestamp.
/// File: Stations.cpp
[ ... ]
void tsunami_lab::io::Stations::write( const t_real* i_totalHeight )
{
for( const Station& station : m_stations )
{
// map station index to cell index
t_idx l_cellIndexX = roundf( ( m_nx / m_scaleX ) * station.m_x );
t_idx l_cellIndexY = roundf( ( m_ny / m_scaleY ) * station.m_y );
t_idx l_cellIndex = m_stride * l_cellIndexY + l_cellIndexX;
std::ofstream l_file;
l_file.open( station.m_path, std::ios::app );
l_file << m_time << "," << i_totalHeight[l_cellIndex] << "\n";
l_file.close();
}
m_time++;
}
2. Providing data and output-frequency
We use the submodule json which allows us to use json format for configuration files.
All we have to do is include the header #include <nlohmann/json.hpp> in all
files in which we want to use json.
To accomplish a time-step independent output-frequency for the stations we use an extra thread in the main.cpp.
/// File: main.cpp
[ ... ]
// initialize stations
tsunami_lab::io::Stations l_stations = tsunami_lab::io::Stations( l_nx,
l_ny,
l_waveProp->getStride(),
l_scaleX,
l_scaleY );
// create a thread that runs the stations write function
std::thread writeStationsThread( writeStations, &l_stations, l_waveProp );
[ ... ]
This thread runs the helper function writeStations.
/// File: main.cpp
[ ... ]
void writeStations( tsunami_lab::io::Stations* stations, tsunami_lab::patches::WavePropagation* solver )
{
while( true )
{
if( KILL_THREAD )
{
break;
}
stations->write( solver->getTotalHeight() );
std::this_thread::sleep_for( std::chrono::seconds( (int)stations->getOutputFrequency() ) );
}
}
[ ... ]
The function needs a reference to our initialized Stations object which summarizes and manages the single stations and another reference to our WavePropagation (whether 1D or 2D) to get the information about current water height for example.
We define a variable KILL_THREAD at the beginning of our main.cpp with initial value false to be able to close
the thread later. If the first if condition inside the while loop is false we call the write method on our stations with
the current water heights of our WavePropagation and thus write to the csv files.
After the main program has finished we set the KILL_THREAD variable to true and wait for the thread.
std::cout << "finished time loop" << std::endl;
// free memory
std::cout << "freeing memory" << std::endl;
delete l_setup;
delete l_waveProp;
// kill thread
KILL_THREAD = true;
// wait for thread
writeStationsThread.join();
std::cout << "finished, exiting" << std::endl;
return EXIT_SUCCESS;
}
3. Solver comparison
The config.json is the same in both cases but the output_frequency of the 1D solver is set to 1 and the output
frequency of the 2D solver is set to 5 because the computation time for this example is approximately 5 times
higher on the 2D solver than on the 1D solver.
X and y are given absolute to the scale (scale x: 100, y: 100), so station 03 with \(x: 50\) and \(y: 50\) is exactly in the middle of the simulation.
{
"output_frequency": 1(5),
"stations": [
{
"name": "station01",
"x": 10,
"y": 50
},
{
"name": "station02",
"x": 30,
"y": 50
},
{
"name": "station03",
"x": 50,
"y": 50
},
{
"name": "station04",
"x": 70,
"y": 50
},
{
"name": "station05",
"x": 90,
"y": 50
}
]
}
Visualization of the 1D symmetrical problem:
Rendered with 500 cells
Stationion |
01 |
02 |
03 |
04 |
05 |
Position |
50 |
150 |
250 |
350 |
450 |
Visualization of the 2D symmetrical problem:
Rendered with 500x500 cells
Stationion |
01 |
02 |
03 |
04 |
05 |
Position |
(50/250) |
(150/250) |
(250/250) |
(350/250) |
(450/250) |
In both cases, the water height is 5 m and at all positions within a radius of 10 m around the centre point, the water height is 10 m.
Comparison on 52 data points per station:
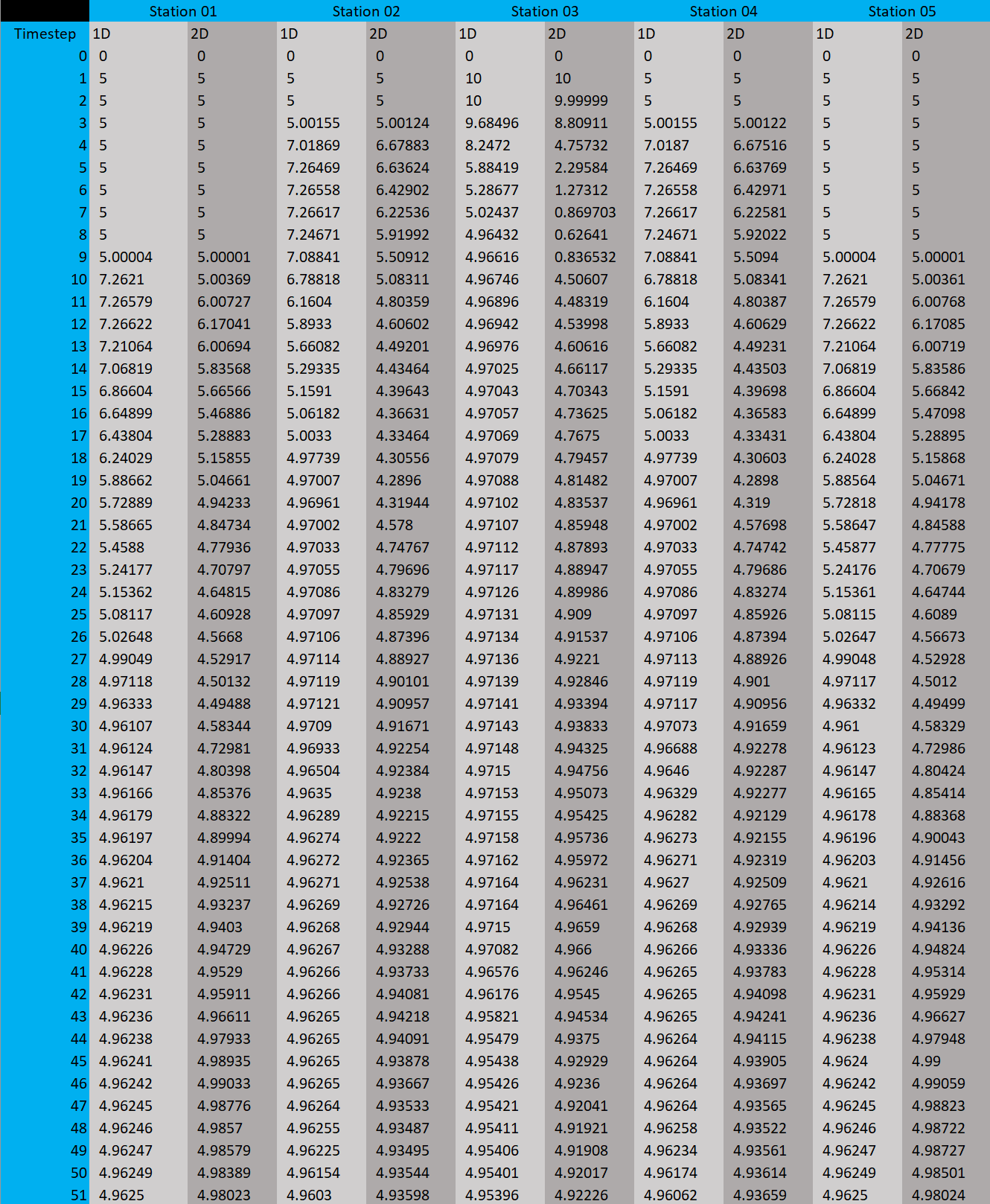
You can clearly see the symmetrical problem in both cases. The values of 1D and 2D are not exactly the same, but they behave very similarly.
Contribution
All team members contributed equally to the tasks.